mathinschool.com
numbers and algebraic expressions
logic, sets, intervals
absolute value
function and its properties
linear function
quadratic function
polynomials
rational function
exponential function
logarithm
number sequences
limits of sequences and functions
derivative and integral of functions
trigonometry
plane geometry
analytic geometry
solid geometry
combinatorics
probability
elements of statistics
kropki game
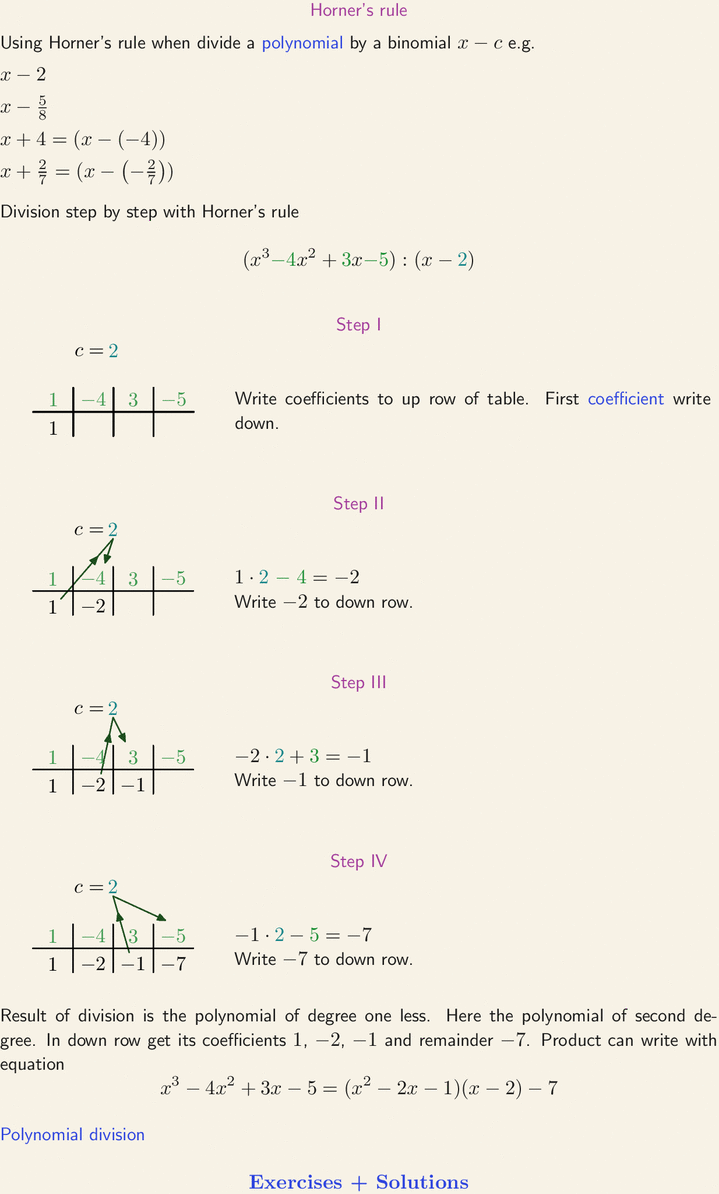
Using Horner's rule when divide a polynomial by a binomial x-c e.g. x - 2, x - 5/8, x+4 = x - (-4), x + 2/7 = x - (-2/7). Division step by step with Horner's rule. (x^3 - 4x^2 + 3x - 5) : (x - 2). Write coefficients to up row of table. First coefficient write down. Result of division is the polynomial of degree one less. Here the polynomial of second degree. In down row get its coefficients 1, -2, -1 and remainder -7. Product can write with equation x^3 - 4x^2 + 3x - 5 = (x^2-2x-1)(x-2) - 7. Polynomial division.