mathinschool.com
numbers and algebraic expressions
logic, sets, intervals
absolute value
function and its properties
linear function
quadratic function
polynomials
rational function
exponential function
logarithm
number sequences
limits of sequences and functions
derivative and integral of functions
trigonometry
plane geometry
analytic geometry
solid geometry
combinatorics
probability
elements of statistics
kropki game
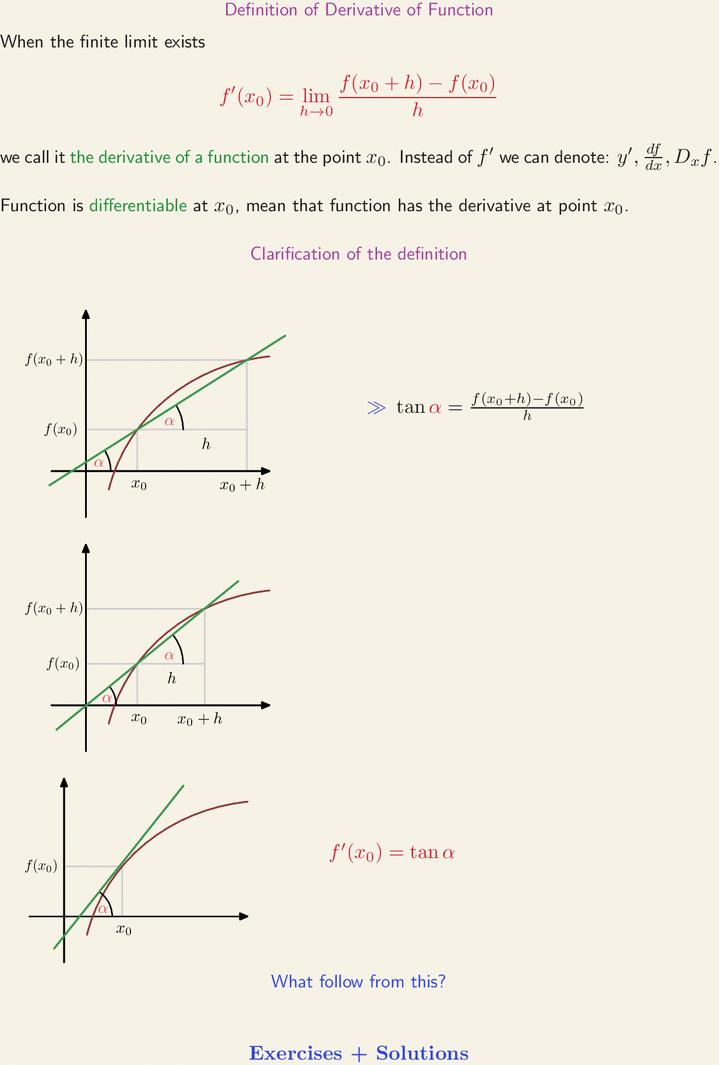
When the finite limit exists f'(x_0) = lim_{h → 0} (f(x_0+h) - f(x_0)) / h we call it the derivative of a function at the point x_0. Instead of f' we can denote: y', df/dx, D_xf. Function is differentiable at x_0, mean that function has the derivative at point x_0. Clarification of the definition tan α = (f(x_0+h) - f(x_0) / h. f'(x_0) = tan α. What follow from this?